The interest in quantum materials is driven by their often novel and unanticipated properties. These are commonly a reflection of strong electron correlations and/or the interplay of multiple relevant energy scales. An important aspect of correlated matter research is the study of model systems that accentuate particular characteristics of quantum materials. These model systems of strong correlations often feature several phases and quantum critical points and perturbative methods are of rather limited use in calculating these properties from the model Hamiltonian.
The tool box to theoretically address the emergent properties of strongly correlated systems include numerical and self-consistent methods, e.g. the non-crossing approximation and various Monte-Carlo schemes but also renormalization group and large-N methods. The standard approach to strong correlations is the dynamical mean field theory which also has been extended in various directions. Quite generally, a whatever works-attitude is often helpful in tackling the challenges posed by strong correlations.
Highlights
“Dynamical scaling of charge and spin responses at a Kondo destruction quantum critical point”
Ang Cai, and Zuodong Yu and Haoyu Hu and Stefan Kirchner, and Qimiao Si
submitted and arXiv:1902.11293v1 (2019)
Quantum critical points often arise in metals perched at the border of an antiferromagnetic order. Recent observation of singular and dynamically scaling charge conductivity in an antiferromagnetic quantum critical heavy fermion metal implicates beyond-Landau quantum criticality. Here we study the charge and spin dynamics of a Kondo destruction quantum critical point (QCP), as realized in a Bose-Fermi Kondo model, using both a dynamical large-N limit and an SU(2)-symmetric continuous- time quantum Monte Carlo method. We find that the critical exponents and scaling functions of the spin and single-particle responses of the QCP in the SU(2) case are essentially the same as those of the large-N limit, suggesting that 1/N corrections are subleading. Building on this insight, we demonstrate that both charge and spin responses at the Kondo destruction QCP are singular and obey ω/T scaling.

Local spin susceptibility χ(τ) at the QCP of (a) the dynamical large-N limit and (b) the SU(2) case; and at the Kondo destruction critical phase of (c) the dynamical large-Nlimit and (d) the SU(2) case. In (a,c), the temperature T is measured in TK0 . In (b,d), β = 1/T .
“Classical and quantum liquids induced by quantum fluctuations”
Miguel M. Oliveira, Pedro Ribeiro and Stefan Kirchner
accepted in Phys. Rev. Lett. and arXiv:1810.10582 (2018)
Geometrically frustrated interactions may render classical ground-states macroscopically degen- erate. The connection between classical and quantum liquids and how the degeneracy is affected by quantum fluctuations is, however, less well understood. We study a simple model of coupled quan- tum and classical degrees of freedom, the so-called Falicov-Kimball model, on a triangular lattice and away from half-filling. For weak interactions the phase diagram features a charge disordered state down to zero temperature. We provide compelling evidence that this phase is a liquid and show that it is divided by a crossover line that terminates in a quantum critical point. Our results offer a new vantage point to address how quantum liquids can emerge from their classical counterparts.

Phase diagram of the FK model on the triangular lattice in the T−U plane for xf =1/3 and xc =2/3. The red start indicates the quantum phase transition between the liquid states. The inset depicts a sketch of the phases in the thermodynamic limit. Band structure assuming CDW order for U = 2 (b) and U = 5 (c).
“Interaction-Tuned Anderson versus Mott Localization”
Andrey E. Antipov, Younes Javanmard, Pedro Ribeiro, and Stefan Kirchner
Phys. Rev. Lett. 117, 146601 (2016)
Disorder or sufficiently strong interactions can render a metallic state unstable, causing it to turn into an insulating one. Despite the fact that the interplay of these two routes to a vanishing conductivity has been a central research topic, a unifying picture has not emerged so far. Here, we establish that the two-dimensional Falicov-Kimball model, one of the simplest lattice models of strong electron correlation, does allow for the study of this interplay. In particular, we show that this model at particle-hole symmetry possesses three distinct thermodynamic insulating phases and exhibits Anderson localization. The previously reported metallic phase is identified as a finite-size feature due to the presence of weak localization. We characterize these phases by their electronic density of states, staggered occupation, conductivity, and the generalized inverse participation ratio. The implications of our findings for other strongly correlated systems are discussed.
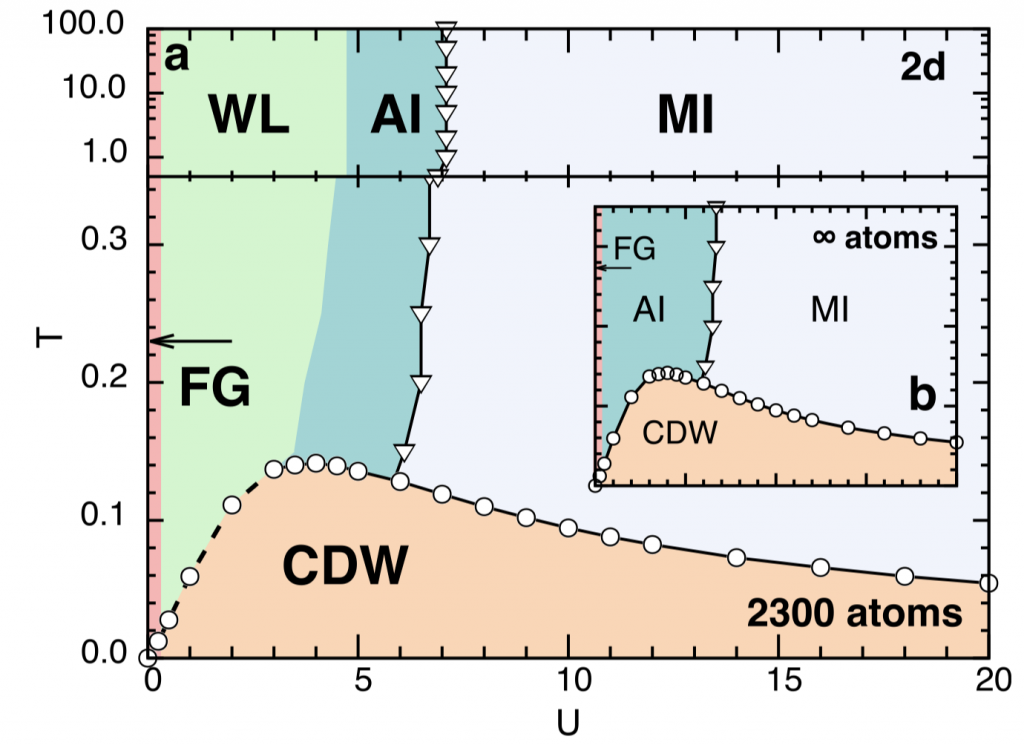
Phase diagram of the particle-hole symmetric FK model in 2d in the U-T plane, obtained by lattice Monte Carlo calculations, consisting of different phases: Fermi gas (FG) at U 1⁄4 0, charge-density wave insulator (CDW) at a low temperature, and all nonzero values of U. High-temperature phases: Anderson insulator (AI) at intermediate values of U crossing over to a weakly localized (WL) at smaller U, Mott-like insulator (MI) at large U. The points and lines show phase boundaries; the dashed line indicates the first- order phase transition between WL and CDW phases. Inset: Extrapolation to the thermodynamic limit.