The interest in understanding the dynamics of strongly correlated systems beyond the linear response regime has grown tremendously in recent years. As a result, there is mounting evidence that quantum matter far from equilibrium possesses interesting and unanticipated properties. On the one hand, the recent interest in non-equilibrium properties of quantum matter is fueled by advances in creating such states in a controlled fashion through.
Nonequilibrium quantum dynamics, e.g. can be studied in adiabatically isolated optical traps and well characterized non-equilibrium states in open systems are frequently investigated in nano-structured systems. On the other hand, a growing number of spectroscopic investigations are based on pump-probe or time-resolved techniques.
For quantum critical systems with their scale-invariant spectrum, i.e. in the absence of any intrinsic scale, any perturbation may probe the system in the nonlinear regime beyond the validity of the fluctuation-dissipation theorem. Understanding non-equilibrium response is thus of practical importance. Yet, there is at present no generally accepted theory to organize the quantum critical dynamics far from equilibrium in terms of universality classes.
The quest for a unified understanding of different classes of quantum materials has led to the notion of quantum critical points as an economic and powerful way of describing the phase diagram of quantum matter.
Highlights
“Mixed-order symmetry-breaking quantum phase transition far from equilibrium”
T. O. Puel, S. Chesi, S. Kirchner, and P. Ribeiro
accepted in Phys. Rev. Lett. and arXiv:1809.07219 (2018)
We study the current-carrying steady-state of a transverse field Ising chain coupled to magnetic thermal reservoirs and obtain the non-equilibrium phase diagram as a function of the magnetization potential of the reservoirs. Upon increasing the magnetization bias we observe a discontinuous jump of the magnetic order parameter that coincides with a divergence of the correlation length. For steady-states with a non-vanishing conductance, the entanglement entropy at zero temperature displays a bias dependent logarithmic correction that violates the area law and differs from the well-known equilibrium case. Our findings show that out-of-equilibrium conditions allow for novel critical phenomena not possible at equilibrium.

(a) Schematic picture of the Ising transverse field spin chain in contact with the magnetic reservoirs. (b) Phase diagram as a function of the magnetization potentials mL and mR. The color coding depicts the qualitative value of the current used to classify the phases (see Fig. 2(a)). (c) Correlation length along the red-dashed line in panel (b). The inset shows the scaling of ξ near the transitions at mR = ±m1. (d) Order parameter along the same line of panel (c).
“The renormalized superperturbation theory (rSPT) approach to the Anderson model in and out of equilibrium”
Enrique Muñoz, Farzaneh Zamani, Lukas Merker, Theo A. Costi, and Stefan Kirchner
J. Phys.: Conf. Ser. 807, 092001 (2017)
The properties of current-carrying steady states of strongly correlated systems away from the linear-response regime are of topical interest. In this article, we review the renormalized perturbation theory (rSPT), or renormalized SPT of reference [1] for the Anderson model. We present an extension to higher orders and compare the higher-order results with NRG calculations. Finally, we elucidate the role of Ward identities in calculating out-of-equilibrium properties and address claims made in the literature.
[1] Muñoz, E. and Bolech, C. J. and Kirchner, S. Phys. Rev. Lett. 110 016601 (2013)

The transport coefficient cT versus the asymmetry parameter εd/∆: Continuous lines are the renormalized rSPT results including higher-order terms. Dashed lines are the renormalized rSPT results at the lowest order. Symbols are the NRG results for the same set of parameters. The particle-hole symmetric reference system is located at εd = −U/2.
“Steady-State Dynamics and Effective Temperature for a Model of Quantum Criticality in an Open System”
P. Ribeiro, F. Zamani, and S. Kirchner
Phys. Rev. Lett. 115 220602 (2015)
We study the thermal and nonthermal steady-state scaling functions and the steady-state dynamics of a model of local quantum criticality. The model we consider, i.e., the pseudogap Kondo model, allows us to study the concept of effective temperatures near fully interacting as well as weak coupling fixed points. In the vicinity of each fixed point we establish the existence of an effective temperature—different at each fixed point—such that the equilibrium fluctuation-dissipation theorem is recovered. Most notably, steady- state scaling functions in terms of the effective temperatures coincide with the equilibrium scaling functions. This result extends to higher correlation functions as is explicitly demonstrated for the Kondo singlet strength. The nonlinear charge transport is also studied and analyzed in terms of the effective temperature.
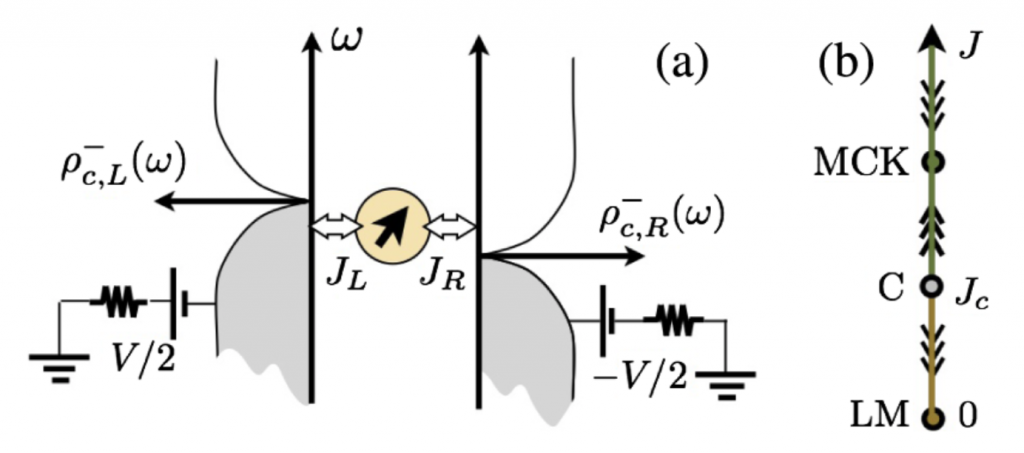
(a) Sketch of the model: a spin interacts with two fermionic leads which are characterized by their respective density of states ρ−{c;L/R}(ω) and chemical potentials μ{L/R}. (b) Phase diagram of the multichannel PKM with gap exponent r < r{max}: A QCP (C) separates the multichannel Kondo (MCK) fixed point from the (weak-coupling) local moment (LM) fixed point.